Search This Blog
Data in science, Stats, Coding and Brain Imaging
Thoughts, opinions, code with a zest of brain imaging and open science.
Posts
Latest posts
Rewriting history - Git history that is
- Get link
- Other Apps
EU scientific data processing and sharing (2/2)
- Get link
- Other Apps
EU scientific data processing and sharing (1/2)
- Get link
- Other Apps
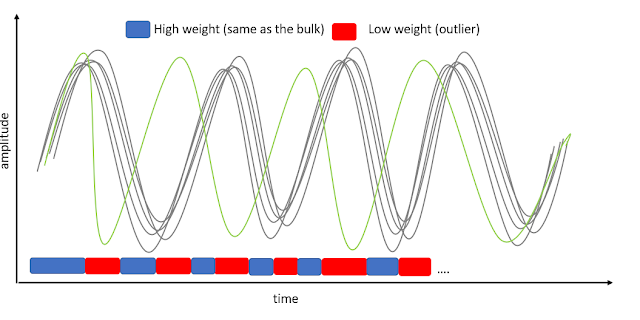
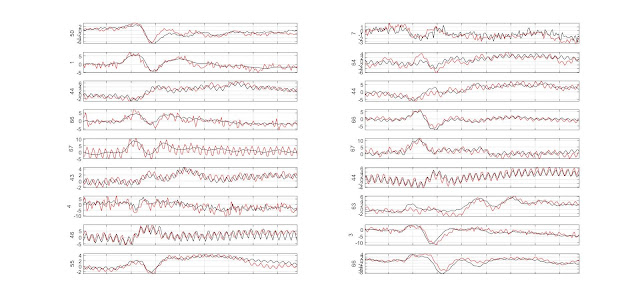
GLM single trial weighting for EEG
- Get link
- Other Apps